データ分析の書記録

読んだ本の内容って忘れてしまいますよね。このブログは分析関係の読んだ本、勉強したことの記録です。

調査観察データの統計科学　５章：選択バイアス

因果推論

はじめに

前回の話 shinomiya-note.hatenablog.com

5.1 選択バイアス

以下の図をご覧ください。

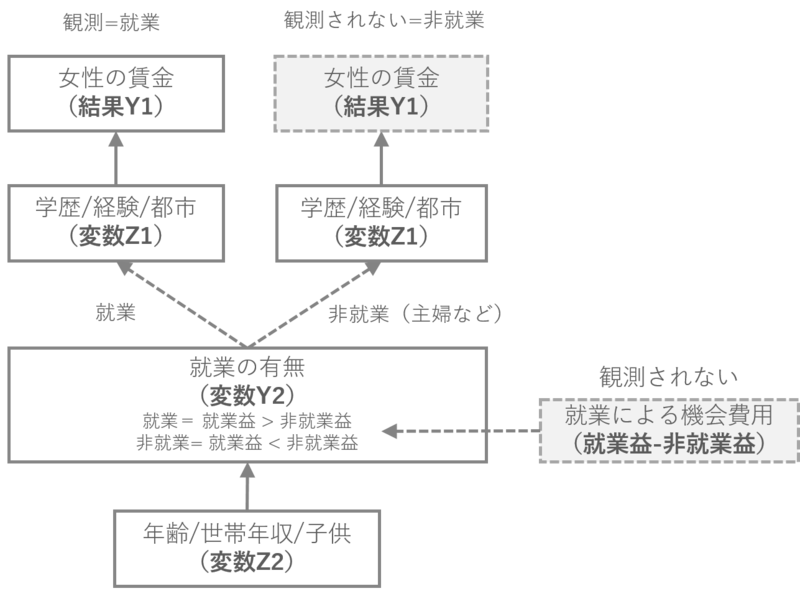
f:id:shinomiya_note:20200312183854p:plain:w500

賃金（Y1）は働いている人しかもらえません＝観測できません。働くかどうか（Y2)は各人の年齢/世帯年収/子供等の変数（Z2)により考えた結果、働いた方が利益がある場合に就業します。
さて、非就業の観測されない賃金バイアスを補正し、真の女性の賃金を知りたいとします。

5.2 プロビット選択モデル

このようなケースの時、ヘックマンらが整備したプロビット選択モデルを使います。
まずは例のごとく、「観測されない＝欠測値」のデータ補正のためのY1とY2のモデルを考えパラメータの推定をしてやります。つまり”尤度（の関数）”を考えます。 そのためにY1：賃金の回帰モデルとY2：就業のプロビット回帰モデルの2つの回帰モデル（とパラメータ）を考えます。
統計モデルですので、予測子とリンク関数、誤差の分布を決めてやればよいわけですね。パラメータの記号などは自分でわかりやすいように本とは一部変えています。

賃金の回帰モデルとパラメータ

\begin{align} y_1 = z_1\beta_1+ε_1 \end{align}

就業のプロビット回帰モデルとパラメータ

\begin{align} y_2= z_2\beta_2+ε_2 \end{align}

2つの回帰モデルの誤差εのモデル（多変量正規分布）

\begin{align} \begin{pmatrix} ε_1 \\ ε_2 \end{pmatrix} ～ N( \begin{pmatrix} 0 \\ 0 \end{pmatrix}, \begin{pmatrix} σ^2_{1} & ρσ_1 \\ ρσ_2 & 1 \end{pmatrix} ) \end{align}

プロビット選択モデルはロジスティック回帰と同様に0～1の範囲のデータに使用するものです。ここでは就業の有無=(0,1)ですね。標準正規分布の累積分布関数を用います（リンク関数自体はロジスティック回帰同様、逆関数であるプロビット関数を使う）。 また、尤度は欠測のメカニズム3タイプによって変わりましたので、それも考慮してやります。

欠測のタイプ

本ケースでは、真の目的である賃金（Y1）がY1>0（賃金がある）と観測されることで、就業するか否か（Y2=(0,1)）が決まります。この条件はランダムでない欠測（NMAR）*にあたります。その時の尤度は \begin{align} p(y_{obs},m|θ,Φ)&=∫p(y|θ)p(m|y,Φ)dy_{miss} \\ &=\prod_{i:m=1}p(y_{i}|θ)p(m_{i}|y_{i},Φ) \prod_{i:m=0}∫p(y_{i}|θ)p(m_{i}|y_{i},Φ)dy_{i} \end{align} でした（m：観測の有無変数ｍ=(0,1)）。

* 欠測するかは結果Yや他の変数に関係する

尤度関数

p(y|θ) = p(y_1|β_1)

p(m|y,Φ)=p(y_2|y_1,β_2)

ここで観測の有無変数ｍ=0,1→y2=0,1の観測と欠測に分けると \begin{align} p(y_{1obs},y_2|β_1,β_2) &=\prod_{i:y_{i2}=1}p(y_{i1}|β_{1})p(y_{i2}|y_{i1},β_{2}) \prod_{i:y_{i2}=0}∫p(y_{i1}|β_{1})p(y_{i2}|y_{i1},β_{2})dy_{i1} \\ &=\prod_{i:y_{i2}=1}p(y_{i1}|β_{1})p(y_{i2}|y_{i1},β_{2}) \prod_{i:y_{i2}=0}1×p(y_{i2}|β_{2}) \\ &=\prod_{i:y_{i2}=1}p(y_{i1}|β_{1})p(y_{i2}=1|y_{i1},β_{2}) \prod_{i:y_{i2}=0}p(y_{i2}=0|β_{2}) \\ &=\prod_{i:y_{i2}=1}[\frac{1}{σ_1}φ(\frac{y_{i1}-x^t_{i1}β_1}{σ_1})×Φ(\frac{1}{\sqrt{1-ρ^2}}\{x^t_{i2}β_2+\frac{ρ}{σ_1}(y_{i1}-x^t_{i1}β_1)\})]\prod_{i:y_{i2}=0}[1-Φ(x^t_{i2}β_2)] \end{align}

になります。Φ(・)が標準正規分布の累積分布関数、φ(・)標準正規分布の確率密度関数です。ここ部分が良く分からなかったので、次項で補足しています。

補足

尤度を求めるにあたって、賃金が観測されたうえでの就業の有無の確率分布P(y2>0|y1)が正規分布の累積分布関数に従い、賃金の確率分布P(y1)が正規分布に従う、というのが今回のキモです。 正規分布の累積分布関数は、確率密度関数を積分し、範囲-∞～aの領域で囲まれた面積=確率をだしているにすぎません。ようはaはどこまでの範囲を入れるか？という指定です。

\begin{align} F(a)=\int_{-∞}^{a} \frac{1}{\sqrt{2\piσ^2}}e^{-\frac{(x-μ)^2}{2σ^2}}dx \end{align} ですが、標準化するので \frac{(x-μ)}{σ}=zに変えておきます。ということは積分の対応区間aも標準化されます。ついでにσもに出しておきます。 \begin{align} F(a)=\int_{-∞}^{\frac{a-μ}{σ}} \frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}(z^2)}\frac{1}{σ}・dx \end{align} \frac{(x-μ)}{σ}=zより、 x=μ+σzと変形し、xの関数（μは定数）として考えてやりzで微分すると、 \frac{dx}{dz}=σとなるので、 \begin{align} F(a)=\int_{-∞}^{\frac{a-μ}{σ}} \frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}(z^2)}dz = Φ(z) \end{align}

Φ(・)が標準正規分布の累積分布関数です。 多重正規分布の条件付き分布の性質が \begin{align} y_2|y_1 =y_{1} ～ N(μ_2+σ_{12}σ_{11}^{-1}(y_1-μ_1),\quad σ_{22}-σ_{12}σ_{11}^{-1}σ_{12}) \quad=\quad N(平均:μ、分散:σ^2) \end{align} なので、 \begin{align}y_2|y_1 ～ N(x_2β_2+\frac{ρ}{σ_1}(y_1-x_1β_1), 1-ρ^2) \end{align} パラメータに入れてやると \begin{align} P(y_2>0|y_1)=Φ(z)=Φ(\frac{1}{\sqrt{1-ρ^2}}(x_2β_2+\frac{ρ}{σ_1}(y_1-x_1β_1))) \end{align}

賃金のP(y1)は、標準正規分布と正規分布の確率密度関数の関係が \begin{align} 標準正規= φ(z)=\frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}(z^2)} \\ 正規= f(x)=\frac{1}{\sqrt{2\piσ^2}}e^{-\frac{1}{2}(\frac{(x-μ)^2}{σ^2})} \\ f(x)=\frac{1}{σ}φ(\frac{x-μ}{σ}) \end{align} となることから、正規分布の確率密度関数を標準正規分布のパラメータzで表現してやるには \begin{align} P(y_1)=\frac{1}{σ_1}φ(\frac{y_1-x_1β_1}{σ_1}) \end{align} となる。